Как измерять и интерпретировать уровень Сигм для оценки возможностей улучшения процессов?
Как сравнивать центры распределения данных с помощью медиан, особенно при наличии ненормально распределенных данных?
Как сравнивать разбросы данных, используя межквартильные диапазоны для более точного понимания вариабельности процессов?
Как применять регрессионное моделирование для ненормально распределенных данных, чтобы повысить точность прогнозирования и анализа?
На эти и другие вопросы ответит Максим Владимирович Соловьёв, Мастер Черных Поясов Лин Шесть Сигма, в рамках нашего нового вебинара.
https://youtu.be/h47MwjPxihk
Ежедневно, при реализации проектов, приходится сталкиваться с различного рода данными: фиксированными, лабораторными, данными клиентов и т.д.
При обработке полученных данных, можно заметить, что не все данные носят нормальный характер. Бывают случаи, когда исследователи пытаются осуществить «подстройку» результатов под нормальные, потому что не знают, что делать с ненормальным распределением. Поэтому в данной статье разберем несколько разновидностей распределения данных, поймем, стоит ли пугаться, если данные ненормальны и рассмотрим инструменты, которые могут помочь провести их анализ.
Нормальное распределение данных
Нормальное распределение данных характерно для количественных данных, на распределение которых влияет множество факторов, либо оно случайно. Нормальное распределение характеризуется несколькими особенностями:
- Оно всегда симметрично и имеет форму колокола.
- Значения среднего и медианы совпадают.
- Соотношение между вероятностью и расстоянием от среднего
Это, в частности, означает, что в пределах одного стандартного отклонения в обе стороны лежат 68.2% всех данных, в пределах двух — 95,5%, в пределах трех — 99,7%
Нормальные данные — это те данные, которые распределяются в соответствии с функцией Гаусса:

p = 3.14159… — число Пи
e = 2.71828… — Экспонента
Для проверки характера распределения данных Minitab располагает рядом инструментов. Например, тест Anderson-Darling или графический анализ Summary Report for Weight.
При проведении теста Anderson-Darling, Minitab предоставляет нам следующую информацию:
- Сравнение частотного распределения реальных данных с теоретическим нормальным распределением, подсчитанным с использованием оценок из выборки для m и s:
- Подсчет статистики теста, так называемой A2 , которая должна быть малой, если теоретическое распределение подходит к распределению данных.
- Расчет значения P (P-value) – это вероятность того, что статистика теста A2 могла бы быть настолько же большой, если бы данные пришли из заведомо нормального распределения. Другими словами, значение P-value – это вероятность того, что данные распределены нормальным образом
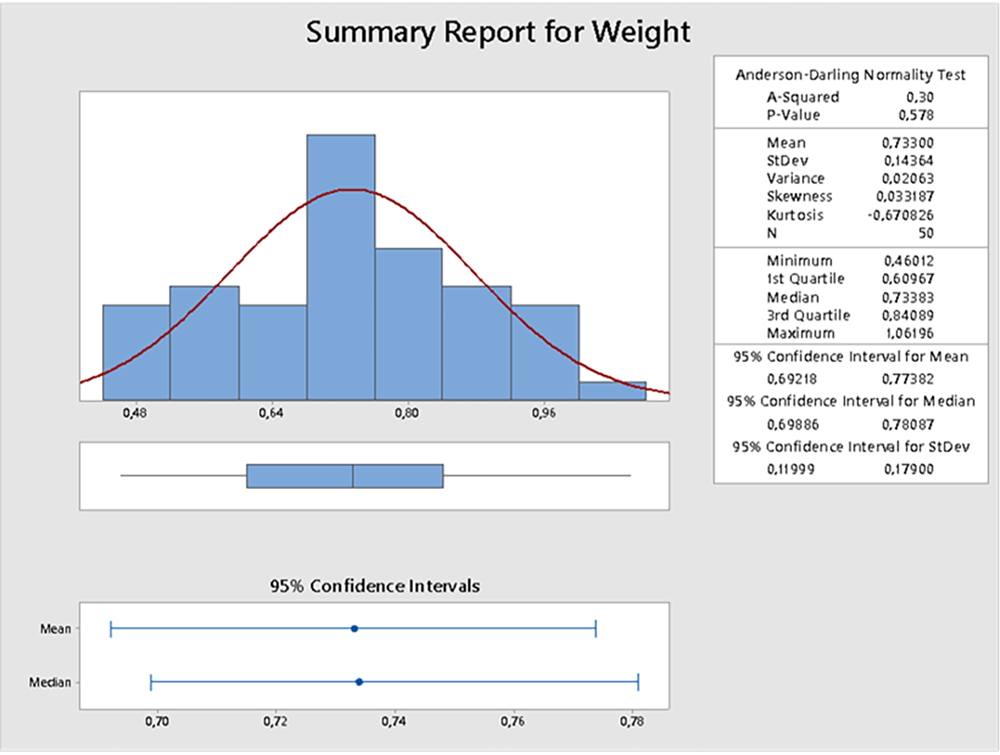
Рисунок 1. Инструмент Summary Report for Weight — график нормального распределения данных
При построении графика с помощью инструмента Summary Report for Weight видно, что нормальное распределение действительно имеет симметричную колоколообразную форму.
К сожалению, нормальное распределение, встречается в нашей работе реже, чем ненормальное.
Ненормальное распределение данных
По видам распределения и использования инструментов анализа, можно выделить 3 области ненормального распределения данных:
Проверка возможности процесса
Для определения характера данных необходимо провести анализ возможностей процесса. Алгоритм анализа представлен на рисунке ниже.
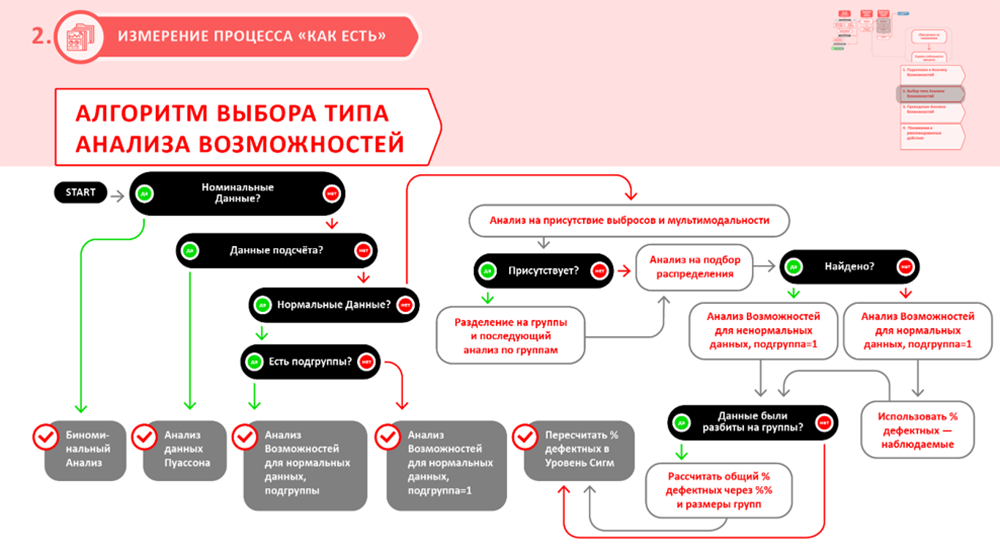
Рисунок 2. Алгоритм анализа возможностей процесса
Если при проверке анализа возможностей выясняется, что данные нормальны, то осуществляется анализ возможностей для нормального распределения данных. Для расчета используются краткосрочные и долгосрочные индексы возможностей. Традиционные методы включают расчет Cp, Pp, Cpk, Ppk. Компания BMGI в своей работе использует значение Z (коэффициент количества сигм).
Если при проверке анализа возможностей выясняется, что данные ненормальны, то для понимания возможности процесса необходимо осуществить ряд операций. Для начала, необходимо разобраться в потенциальных причинах ненормальности и методах возможностей. В таблице представлены данные по категориям причин и их характеристики.
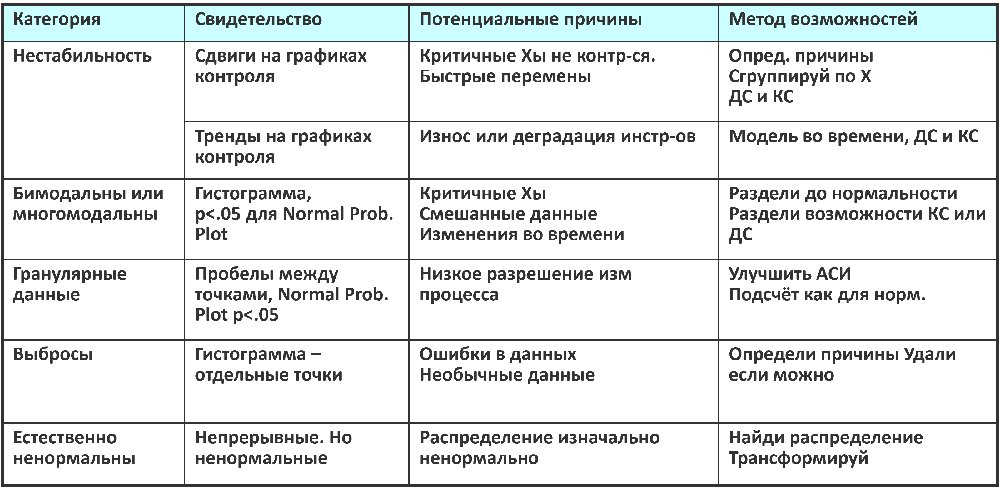
Рисунок 3. Таблица причин ненормальности данных
* Возможности могут быть аппроксимированы переходом в биноминальные если n>500
Пример анализа проверки возможностей процесса:
Шаг 1. Выбор типа анализа возможностей.
Анализ возможностей осуществляется посредством графических инструментов в Minitab.
Обращаем внимание, что гистограмма, полученная Histogram of Time to Antibiotic, имеет не симметричный вид.

Рисунок 4. Инструмент Probability Plot of Time to Antibiotic графический анализ данных.
А графический анализ созданный инструментом Probability Plot of Time to Antibiotic показывает способность соответствия нормальному распределению — 95%. Так же значение AD сильно отличается от нуля — 4,449.В данном случае основным индикатором при проверке статистики будет являться индекс Р – Valuе.Если индекс Р – Valuе меньше 5%, то процесс распределен ненормально.
Из полученных результатов следует вывод: дальнейший анализ данных необходимо проводить по принципу подхода к Gamma распределению, т.к. Johnson Transformation на практике вызывает некоторые сложности в обсуждении данных с заказчиком (заказчик не всегда понимает откуда появился ряд данных, сгенерированных на основе дополнительных коэффициэнтов).
Шаг 3. Для анализа данных Gamma распределения в Minitab используется инструмент Nonnormal Capability Sixpack.
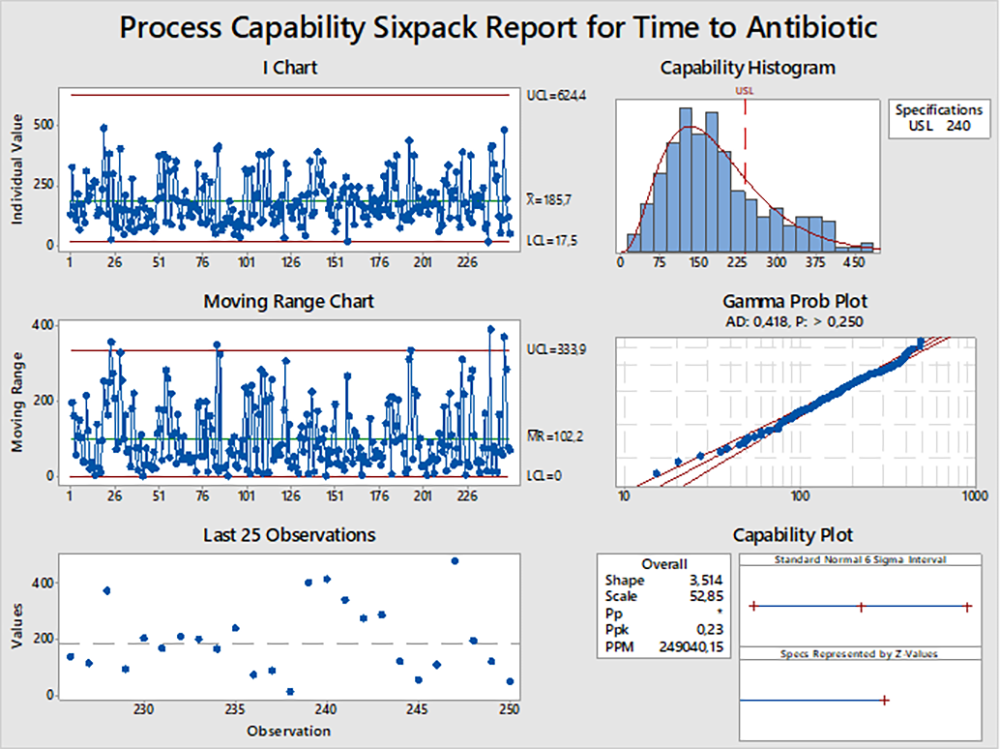
Рисунок 5. Графики контроля Gamma распределения, полученные инструментом Nonnormal Capability Sixpack.
Данный инструмент строит график контроля индивидуальных сдвигов и контроля скользящего диапазона, показывает определяющие показатели при Gamma распределении – значения Формы и Шкалы, а так же дублирует значения коэффициента Р – Valuе и гистограмму Gamma распределения.
Проверка сравнений гипотез
Сравнение центров или разброса данных может понадобиться в случае, когда нам необходимо сравнить данные одного процесса, получаемые из нескольких схожих источников, например разные офисы, разные установки, разное оборудование, разные смены, выпускающие один и тот же продукт или оказывающий один и тот же сервис.
Для сравнения непрерывных ненормальных выборок существует набор инструментов, который представлен в дорожной карте проверки гипотез
Пример анализа сравнений гипотез:
Для того чтобы осуществить анализ необходимо сравнить подгруппы данных по разбросу. Сравнение происходит по вариативности разных подгрупп. В Minitab для этого существует инструмент Test for equal variances.
При построении графика в Test for equal variances обращаем внимание на показатель Levene*s test, который определяет разницу в разбросах для ненормально распределенных данных.

Рисунок 6. Инструмент Test for equal variances график вариативности разных подгрупп
В данном примере коэффициент Р – Valuе меньше 5% -это говорит о том, что в представленной выборке одна из подгрупп отличается от остальных. При сравнении медиан инструмент Levene*s test не подходит. Если необходимо сравнить медианы можно использовать инструмент Mood’s Median test.
После занесения данных в открывшуюся форму, инструмент осуществляет сравнение гипотез, т.е. есть ли разница между медианами выборок данных.

Рисунок 7. Пример сравнения гипотез инструментом Mood’s Median test.
Mood’s Median test показывает количество измерений выше и ниже общей медианы, медианы выборок и их межквартальные диапазоны. Если медиана одной группы попадает на интервал другой, они, вероятно, не различаются значительно. В полученных в данном примере результатах видно, что минимум одна из подгрупп отличается по медиане.
Построение регрессионных моделей
Иногда на практике встречаются процессы, результат которых не нормально распределен. Часто это происходит от того, что неизвестный компонент воздействует на процесс таким образом, что он сильно отклоняется и изменяется. Соответственно, можно предположить, что существует ряд значимых факторов, который ведет к отклонениям данных и наша задача – исключить эти факторы.
В дорожной карте проверке гипотез представлены инструменты для анализа проектов в части моделирования. Обычно данный блок развивается через регрессию данных.
Пример анализа данных с ненормально распределенным результатом:
Шаг1. Проверка Y инструментом Summary Report for Sales.
Шаг2. Поиск факторов, влияющих на процесс отклонения. Для этого проводится естественный регрессионный анализ, который так же показывает возможности управления Y. При получении результатов следует обратить внимание на показатель значимости (регрессия) и коэффициент Р – Value.
Шаг 3. Анализ остатков.Осуществляется посредством инструмента Normal Probabillity Plot.
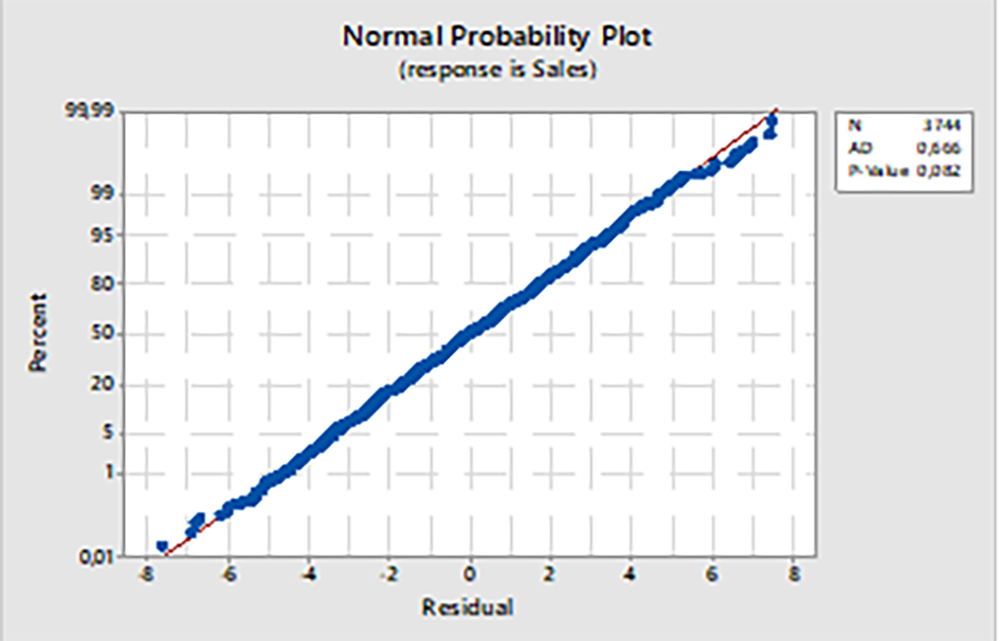
Рисунок 8. Инструмент Normal Probability Plot график распределения остатков
На данном графике можно видеть, что данные по остаткам нормально распределены. Это говорит о том, что при анализе были задействованы все значимые для процесса факторы и теперь есть возможность управлять процессом. Другими словами, неизвестных процессов, которые могут искажать данные больше не осталось.
Данные методы анализа данных входят в обновленную стандартную программу обучения Зеленых и Черных Поясов Lean Six Sigma (LSS) от компании BMGI.